点击上方“五分钟学会算法”按钮，选择“Star”公众号。

重货，尽快发货

来源 | 悟空聊天架构（ID：PassJava666）

前言

《三国杀》是一款结合中国三国时期背景，以身份为线索，以卡牌为形式的热门卡牌游戏，益智休闲兼具，老少皆宜。

在开始之前，我们先来了解一下分布式协议和算法的总体背景。

现在很多开发者对分布式组件的使用有一定的经验，也知道CAP理论和BASE理论的大概含义，但是很少有人认真去研究分布式算法。原因有三：

在后续的文章中我会用故事、通俗的语言给大家讲解分布式算法的原理以及学习路径是怎样的。

学习路径

学习分布式协议和算法的路线可以是先学习四大基础理论作为基础，然后再学习分布式协议和算法，就像在地基上盖房子一样，打好地基之后才能盖出比较稳固的高楼大厦。

四个基本理论：

拜占庭将军问题

CAP 理论

ACID 理论

BASE 理论

八种分布式协议和算法：

Paxos 算法

Raft 算法

一致性哈希算法

Gossip 协议算法

仲裁 NWR 算法

FBFT 算法

POW算法

ZAB 协议

由于篇幅限制，本文仅讨论拜占庭将军问题。

拜占庭将军问题

你可能听说过拜占庭将军问题。这是 Leslie Lambert 提出的点对点通信中的一个基本问题。

拜占庭位于如今的土耳其伊斯坦布尔，曾是东罗马帝国的首都。由于当时拜占庭罗马帝国领土辽阔，为了达到防御的目的，各军队相隔很远，将军之间只能通过信使相互联系。在战争中，拜占庭军队中的所有将军和副官必须达成共识，决定是否有获胜的机会，才能进攻敌营。然而军队中可能会有叛徒和敌方间谍，这就是拜占庭的容错问题。

其实拜占庭问题是分布式领域最复杂的容错模型，理解了它就能掌握分布式共识问题的解决，也能帮助大家理解常用的共识算法，还能帮助我们在工作中选择合适的算法，或者设计合适的算法。

为什么第一个基础理论是拜占庭将军问题？

因为它把分布式系统面临的共识问题抽象的非常好，上面提到的八种分布式算法中，有五种都和拜占庭问题有关，可以说理解了拜占庭问题，以后学习其他算法就会容易很多。

接下来我以三国游戏中的身份牌来解释拜占庭将军问题。

2.1 三国杀身份卡

《三国志》中主要有四种身份：君主、忠臣、叛臣、奸臣。每个玩家都会获得一张身份卡。君主只有1张身份卡。忠臣最多可以有2个身份，奸臣最多可以有4个身份，奸臣最多可以有1张身份卡。

主

领主身份证

胜利条件：消灭所有叛徒和叛徒

Tips：以自身生存为首要目标，分散叛军的注意力，配合效忠派消灭叛军，分清谁是效忠派，谁是内奸。

忠臣

忠诚度身份证

胜利条件：消灭所有叛徒和叛徒，同时保护领主的生存。

技能：忠诚的大臣是领主的盾牌，是震慑反叛者和叛徒的平衡器。

防盗

防盗身份证

胜利条件：消灭领主即可获胜。

Tips：叛军作为人数最多的身份，需要集中火力攻击敌人的弱点，正确的思路是取得胜利的关键。

叛徒

叛徒身份证

胜利条件：先消灭叛军与忠臣，最后与领主决一死战，成为最后的幸存者。

秘诀：正确的策略+冷静的头脑+运气。

2.2 恢复拜占庭问题

东汉末年，袁绍作为盟主，聚集十八个诸侯攻打董卓。董卓被定义为奸臣，袁绍为盟主，还有两个忠臣和一个奸臣。这三个大人物被选中：曹操、刘备、孙坚（孙权的父亲）。奸臣扮演了忠臣的角色。盟主和两个忠臣都不知道奸臣的身份，把他当成忠臣对待。

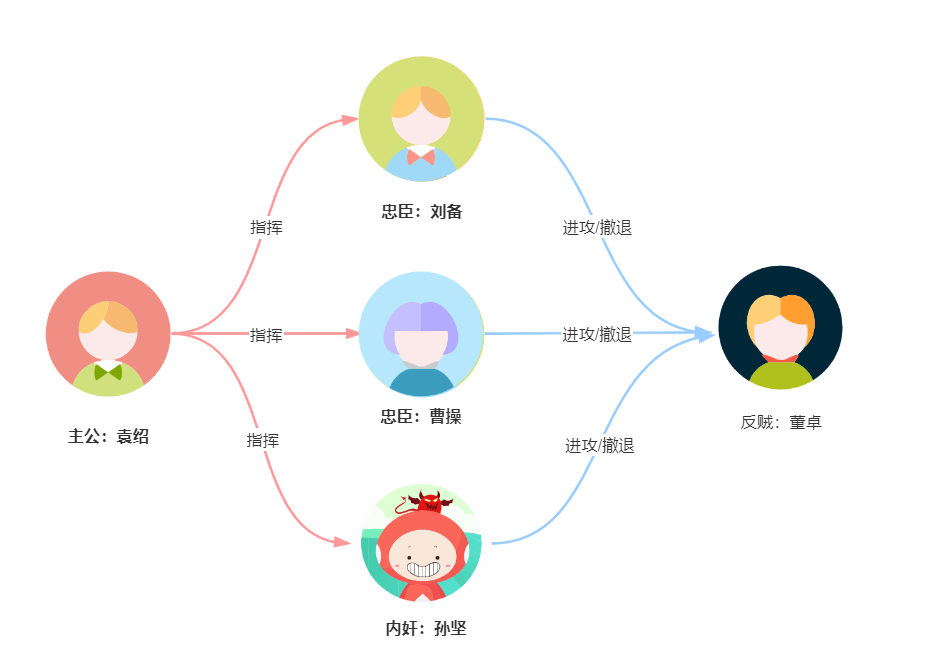
董卓势力很大，西凉士兵精锐，手下还有战神吕布，三雄并立吕布的故事大家都知道，吕布单挑刘备、张飞、关羽。

袁绍为了杀掉董卓，必须统一忠臣的作战计划。三位忠臣不知道还有什么花招，其中一人还是叛徒。如果叛徒暗中与叛军董卓联络，向忠臣发出误导性的战情怎么办？另外，假设这些忠臣通过书信交换战情，如果书信被截获，或者书信中的信息被调换怎么办？这些情景都可能打乱作战计划，最终出现忠臣有的进攻，有的撤退。那么叛军就可以趁此机会发动进攻，逐个突围。

袁绍没有曹操那样的智慧，如何能让手下的忠臣达成共识，制定统一的作战计划？

上述映射关系是拜占庭将军问题的一个简化表达，袁绍现在面临的是一个典型的共识问题，即在可能存在误导信息的情况下，采取合适的沟通机制，让多位将军达成共识，制定一致的作战计划。

2.3 一方选择退出

刘备、曹操、孙坚三人通过信使传递进攻或撤退的信息，再商议进攻或撤退，遵循少数服从多数的原则，不允许弃权。

曹操心生疑虑，在侦察了叛军的地形后决定撤退，而刘备和孙坚则决定进攻。

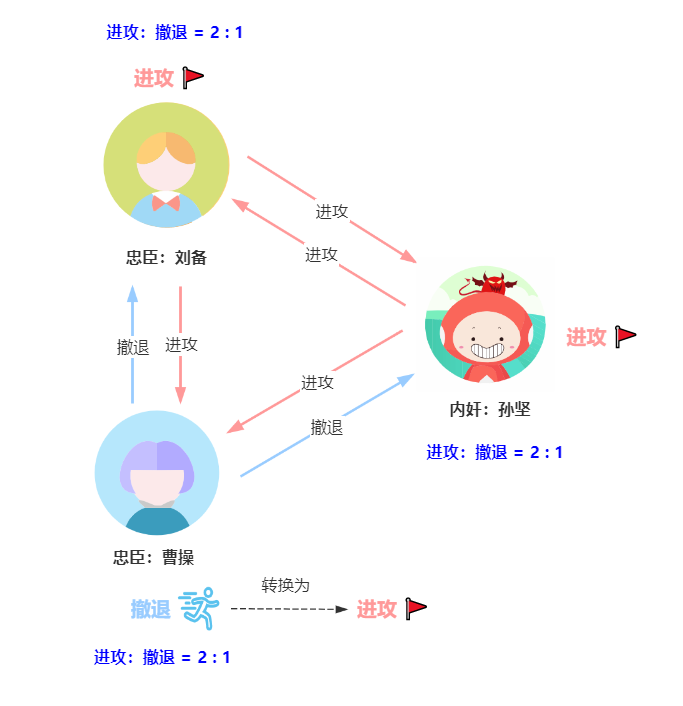
一方选择撤退

曹操得到2票进攻，1票撤退，票数比例为2：1，按照多数决原则，曹操还是会进攻，三方的作战计划都是进攻，所以是一致的，最后打败了董卓。

2.4 叛徒出现——撤退

因为我们前期的设定，孙坚作为叛徒，已经和叛军董卓私下沟通，决定不再攻打董卓。

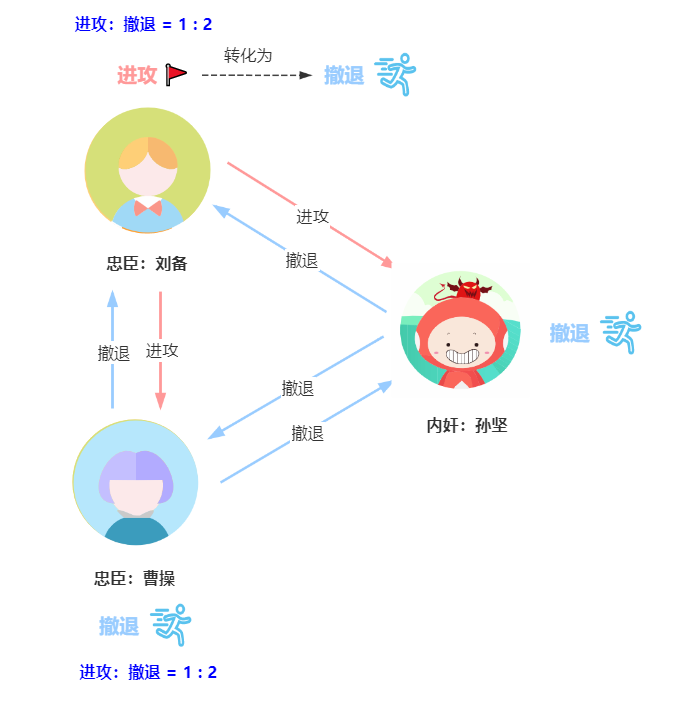
叛徒出现-撤退

刘备进攻和撤退各有一票，他选择了撤退，所以刘备的票数为：进攻：撤退=1：2。按照少数服从多数的原则，刘备最终选择了撤退。那么三方的作战计划都是撤退，所以也是一致的作战计划。

2.5 叛徒的诡计——进一步，退一步

叛徒看过上述计划后，发现忠臣已经全部撤退，并未被消灭，于是想用欺骗的方法除掉其中一名忠臣。

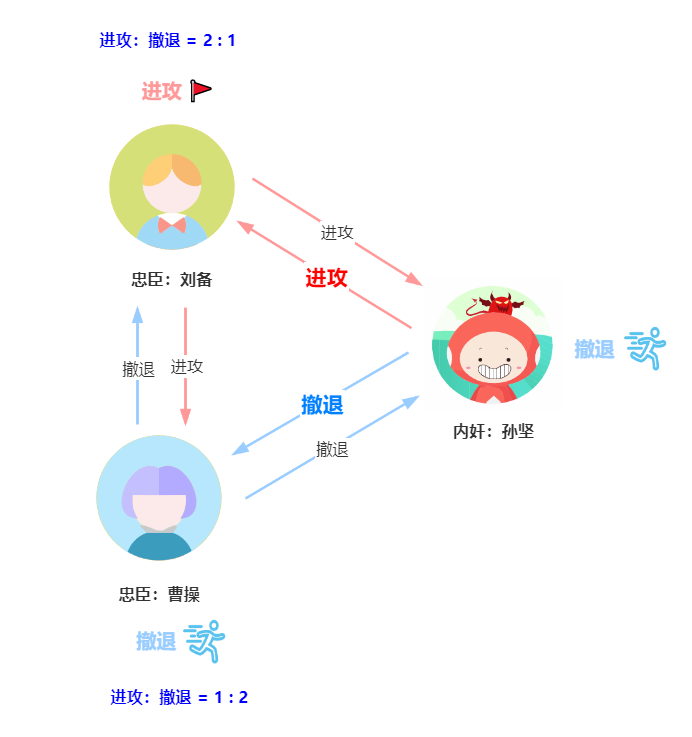
叛徒-进一步退一步

那么结果如何？

刘备的票数是2票进攻1票撤退，曹操的票数是1票进攻2票撤退。按照少数服从多数的原则，刘备最后会选择进攻，曹操会选择撤退。孙坚作为叛徒，肯定不会进攻。刘备孤身一人进攻叛军董卓，但兵力薄弱，被董卓杀死。

从这一幕中我们可以看出，叛徒孙坚通过传递误导性的信息，轻易干扰了刘备和曹操的作战计划，导致两位忠臣被逐一击败。这种现象就是二忠一判的问题。那么主公袁绍该如何解决这个问题呢？

拜占庭问题解决方案

解决方案1 ​​原理

也就是把袁绍也算进去投票，这样就增加了一个忠臣。三个忠臣，一个叛徒。然后四位将军达成协议，如果没有接到命令，就执行默认命令，比如撤退。另外约定的流程是发送作战信息，以及如何执行作战命令。这个方案的重点是进行两轮作战信息协商。

3.1 袁绍担任统帅

让我们看一下第一轮的情况。

首先发送战斗信息的将军称为统帅（袁绍），其他将军称为副官（刘备、曹操、孙坚）。

指挥官将他的战斗信息发送给所有副官。

各个副官会以收到指挥官下达的作战信息作为自己的作战命令；若没有收到指挥官下达的作战信息，则以默认撤退作为作战命令。

我们用一张图来演示一下：袁绍作为领主，首先发出作战信息，并下达作战进攻命令。随后曹操、刘备、孙坚三人都收到了作战进攻命令。

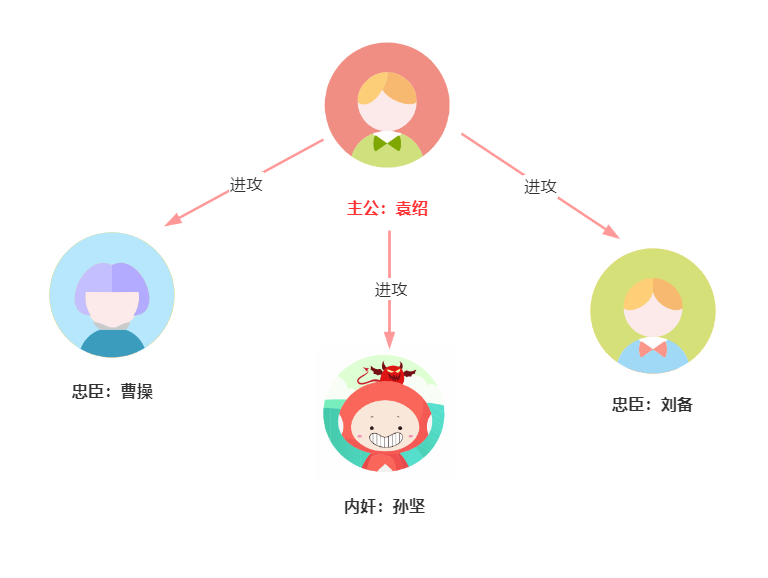
第一回合

让我们看看第二轮是如何进行的。

第一轮统帅（袁绍）已经发出命令，现在刘备、曹操、孙坚需要轮流担任统帅，向另外两名副将发出作战信息。

随后三名副将按照少数服从多数的原则，执行接到的作战命令。

孙坚作弊——两次撤退

例如，如果孙坚作弊，向曹操和刘备都发送撤退信息，如下图所示，那么刘备和曹操将分别获得 2 票进攻和 1 票撤退。根据少数服从多数的原则，刘备和曹操最终将实施进攻，实现作战计划的一致性。曹操和刘备将共同作战，击败叛军董卓（尽管孙坚没有参加战斗）。

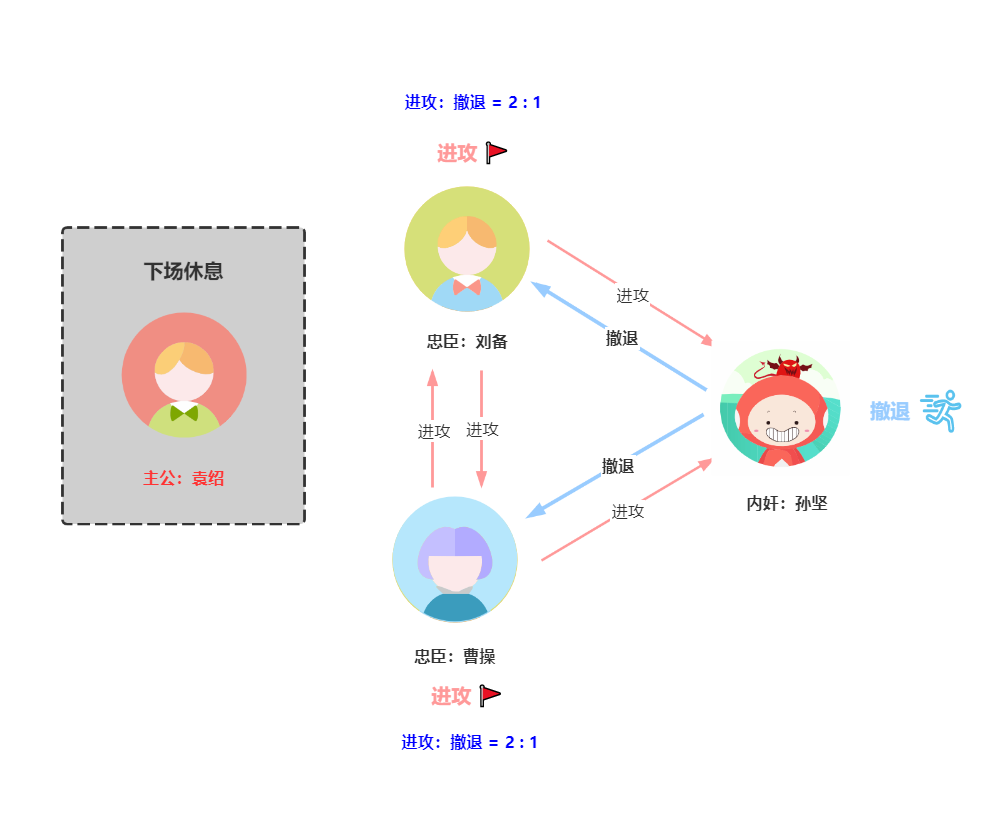
孙坚作弊——两次撤退

孙坚秘籍——一进一退

如果孙坚作弊，给曹操发出撤退命令，给刘备发出进攻命令，那么刘备收到的战斗信息是3票进攻，一定会进攻，而曹操收到的战斗信息是2票进攻，1票撤退，曹操最终还是会进攻，所以刘备还是会和曹操联手，打败了董卓叛军。

看来引入统帅，确实能避免孙坚作弊，但如果第一轮孙坚是统帅，其他人是副官呢？

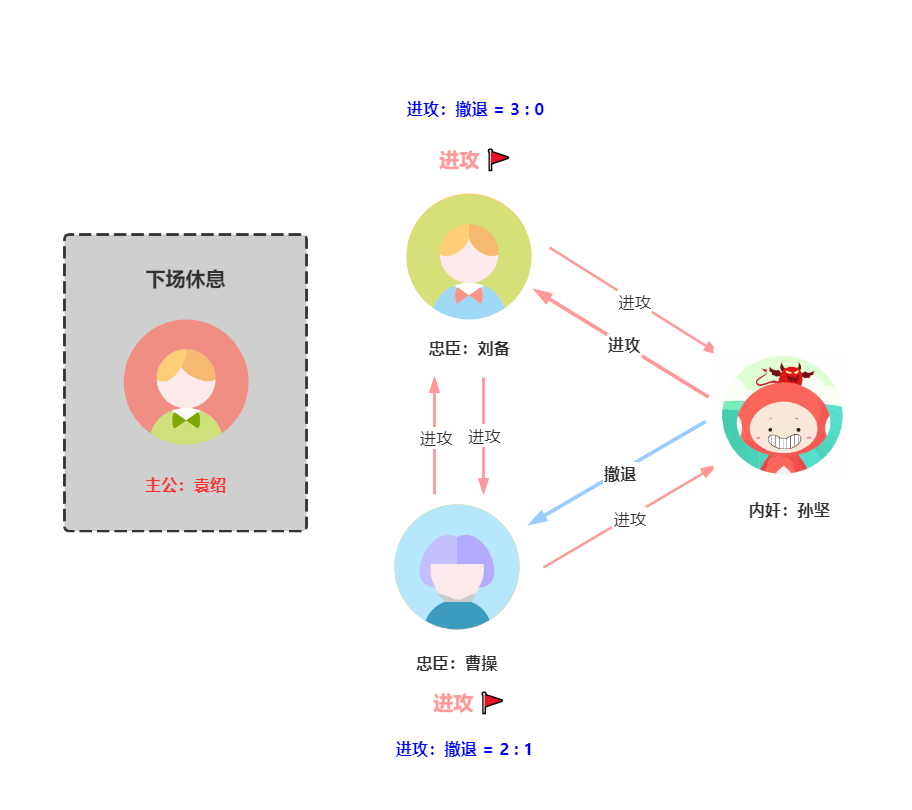
孙坚秘籍——一进一退

3.2 孙坚为将军

第一轮，孙坚向他的一位副将袁绍发出撤退命令，向另外两位副将曹操和刘备发出进攻命令。第一轮结果如下：

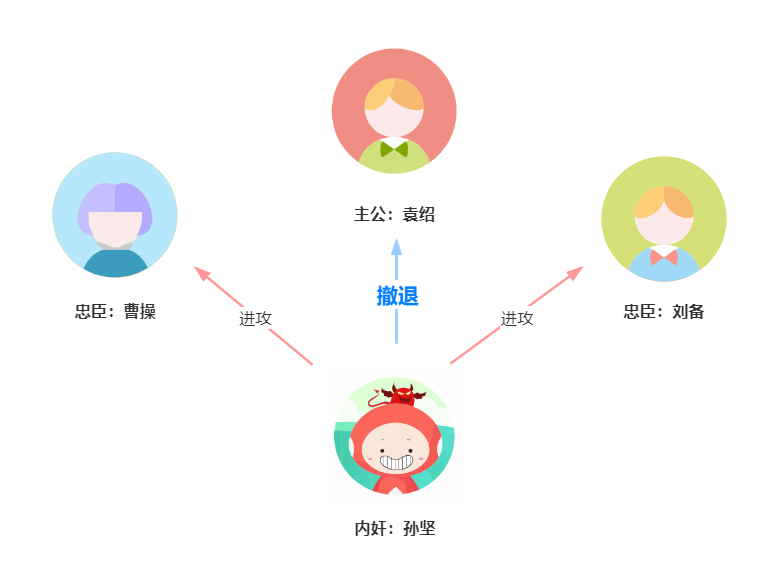
第一回合

第二回合，孙坚休息了一下，其他副官开始按照孙坚发来的指令，给其他副官发出指令。

曹操向刘备、袁绍发出进攻命令。

刘备向曹操、袁绍发出进攻命令。

袁绍向曹操、刘备发出撤退命令。

如下图所示，曹操、刘备、袁绍三方最终分别获得了2票进攻和1票撤退，按照少数服从多数的原则，三方均发起进攻，并执行了一致的作战计划，确保了胜利。

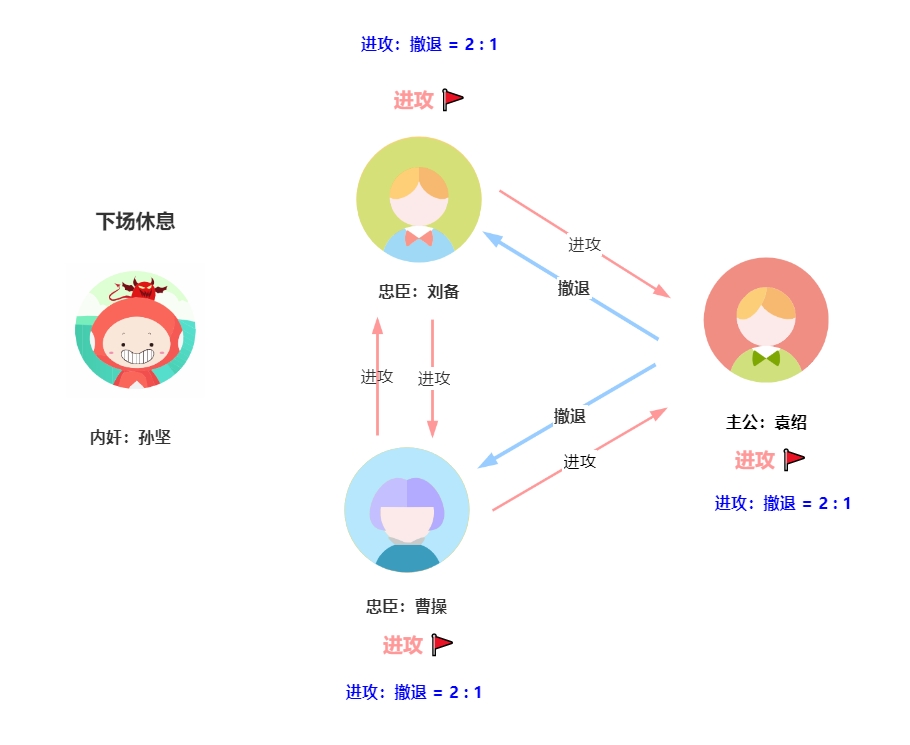
第二轮

3.3 总结

通过上面的演示，我们知道了如何解决拜占庭将军问题。其实 Lambert 在他的论文中也提到了如何解决这个问题。

如果叛军将军人数为m，将军人数n>=3m+1，那么拜占庭将军问题就能解决。

前置条件：叛军将领数量相同，且需要m+1轮战斗谈判。

你只要记住这个公式就可以了，推导过程可以参考论文。

比如上述讨董卓一役，曹操、刘备、孙坚三人中，孙坚是个叛徒，能作弊，使作战计划不一致，必须加上忠臣袁绍来商议共识，才能达成一致的作战计划。

拜占庭解决方案 2-签名

是否可以在不增加忠臣数量的情况下解决拜占庭两名忠臣和一名法官的问题？

方案二是使用签名消息。例如，将军之间通过印章、老虎令牌等令牌进行通信。为了确保以下特性：

限于篇幅，这里就不展开签名演示了。

总结

我们用《三国》里的人物来解释一下分布式系统中的共识场景，他们和分布式系统之间的映射关系是怎样的呢？

别小看拜占庭问题，它是分布式场景中最复杂的故障场景，比如这些知识点在数字货币的区块链技术中都有用到，而且必须用到拜占庭容错算法（BFT）。

另外还有拜占庭容错算法，FBFT算法，PoW算法等，当然我这篇文章里就不讲这些算法了，后面再讲。

有了拜占庭容错算法，就一定有非拜占庭容错算法。顾名思义，就是不存在发送误导信息的节点。CFT 算法解决的是分布式系统存在故障，但不存在恶意节点的场景下的共识问题。简单来说，就是可能因为系统故障导致消息丢失或者重复，但是不存在错误消息或者伪造消息。对应的算法就是 Paxos 算法、Raft 算法、ZAB 协议。后续解释~ 上面提到的 5 个算法都和拜占庭问题有关。大家觉得我们今天讲的拜占庭问题重要吗？

这么多算法该如何选择？

如果节点值得信任，则选择非拜占庭容错算法。否则，使用拜占庭容错算法，例如区块链中使用的 PoW 算法。